玻璃幕墙装饰扣盖防脱落应用技术研究(一)——试验、分析及计算公式
作者:幕墙工程网 时间:2022-07-02 11:06:12

调研发现,玻璃幕墙工程破坏案例中装饰扣盖的破坏占比达到10%以上,本文通过有限元模拟、试验测试和理论分析,对玻璃幕墙咬合型装饰扣盖破坏机理进行研究,并给出了咬合型装饰扣盖的装配力和分离力理论计算公式。玻璃幕墙装饰条的种类很多(见图1),根据不同的分类规则大致可以分类如下:(1) 从材质上,可以分为金属装饰条、陶棍、木装饰条、玻璃装饰条等;(2) 从功能上,可以分为遮阳装饰条、普通装饰条;(3) 从与幕墙系统的关系上,可以分为扣盖类和外加构件类。
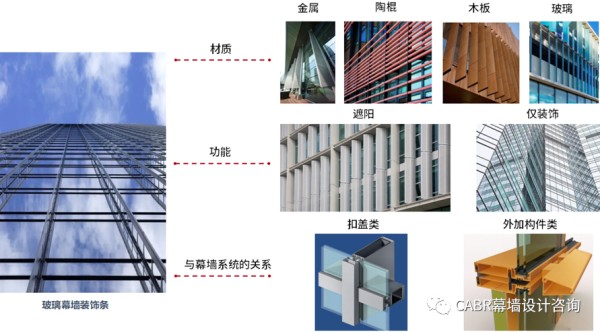
装饰扣盖是玻璃幕墙中最常见的一个构件,特别是咬合型的装饰扣盖,见图2,在明框幕墙、半隐框幕墙中大量使用,其特点是装饰扣盖本身不承担自身以外的荷载;仅靠压板和扣盖挤压配合连接。
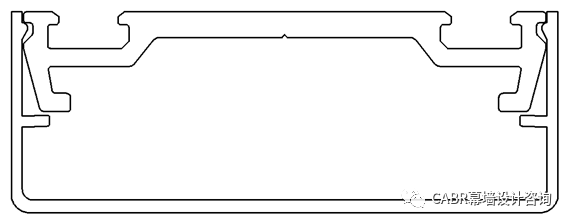
依托于我司承担的“十三五”国家重点研发计划课题“城镇建筑围护结构防高空坠落及安全性能提升关键技术”,调研和统计发现,在所有玻璃幕墙工程破坏案例中,装饰扣盖的破坏占比达到10%以上,其中很大一部分就是上述的咬合型装饰扣盖。调研中发现,有些工程项目的装饰扣盖出现大量松动甚至掉落情况,经过剖析可知,这些装饰扣盖的破坏原因主要有以下几种:(1) 单元式幕墙扣盖在安装过程中,被相邻板块磕碰造成松动;(2) 扣盖设计不合理,没有设置预变形,导致安装松动;(3) 不按图纸施工,本应通长的幕墙压板变成分段设置,由于各段压板不对齐,导致扣盖仅与个别压板连接,承载性能极大削弱;(4) 扣盖过大,侧向风荷载超过扣盖与压板连接的承载力。扣盖虽小,但是破坏坠落以后引发的后果比较严重。由于其不是幕墙系统中的主要受力构件,在设计和施工中往往容易被轻视,在以往的研究中也鲜有专门的研究,在现行的规范中也缺乏细致的规定。为了装饰扣盖能够得到更加规范、安全地应用,我司开展了玻璃幕墙装饰扣盖应用技术研究。本研究基于试验测试、理论分析、有限元模拟和公式推导等方法,研究了装饰扣盖的破坏机理、影响因素效率、安全性能提升措施。本期主要介绍破坏机理和理论公式部分。有限元模拟的分析对象为应用广泛的S60型扣盖(按宽度命名),见图3。
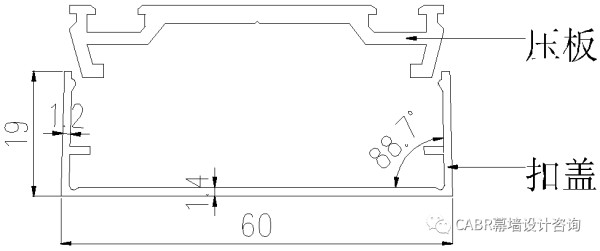
图3 S60型扣盖
采用ANSYS软件进行分析,模型设置为实体单元,在扣盖与压板之间在法向上设置软接触,摩擦系数μ=0.165;S60扣盖和配套压板模型长度300mm,装配过程中的插入角α=15°,分离过程中的分离角β=29.23°,见图4;采用位移加载的静力分析,0~1s为装配过程,1~2s为分离过程。
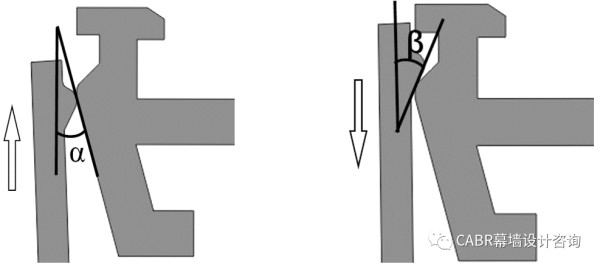
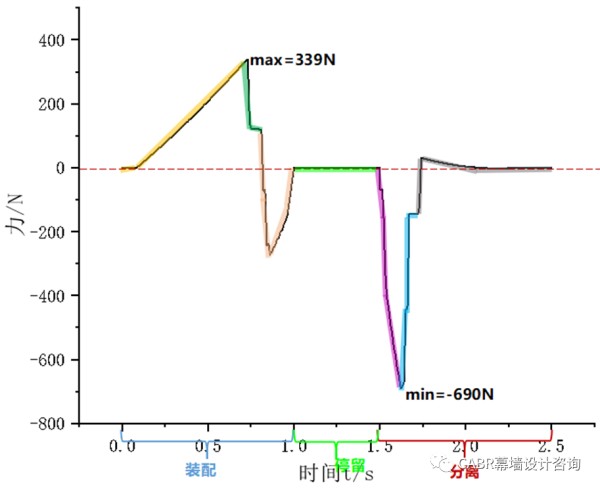
第一阶段,在扣盖与压板接触后,随着位移加载增大,悬臂钩的变形逐渐增大,加载力与加载位移几乎呈线性关系,达到下图所示位置时,加载力出现最大值,为338.96N;第二阶段,加载点反力值迅速减小,此时,扣盖与压板的竖直面接触,悬臂钩变形不再增加,呈滑动摩擦状态;第三阶段,在继续加载时,悬臂钩进入压板凹槽,此时由于悬臂钩的变形很大,偏斜力很容易克服摩擦力,因此发生比较大的突变,加载点反力的数值几乎反号,随着位移加载增大,悬臂钩变形逐渐减小,反力也逐渐减小最终完成装配。值得注意的是,第三阶段在实际安装时并不存在,因为在第二阶段完成之后,扣盖即可自动咬合入凹槽,安装到位。分离过程与装配过程相似,由于分离角度大于插入角度,因此曲线斜率很大,同时,分离时所需要的最大反力也更大,为689.51N;当达到峰值后,悬臂钩变形不再增大,仅剩动摩擦力起作用,反力迅速减小,出现一个小的平直段,在此之后可认为扣盖与压板发生分离,达到破坏状态。在装配和分离过程中,扣盖应力未达到屈服应力,与理论分析时的材料处于弹性阶段假设相符。为验证有限元模拟的正确性,采用相同规格的型材进行扣盖装配和拆卸,作为对比试验。试验通过万能试验机进行,见图6。

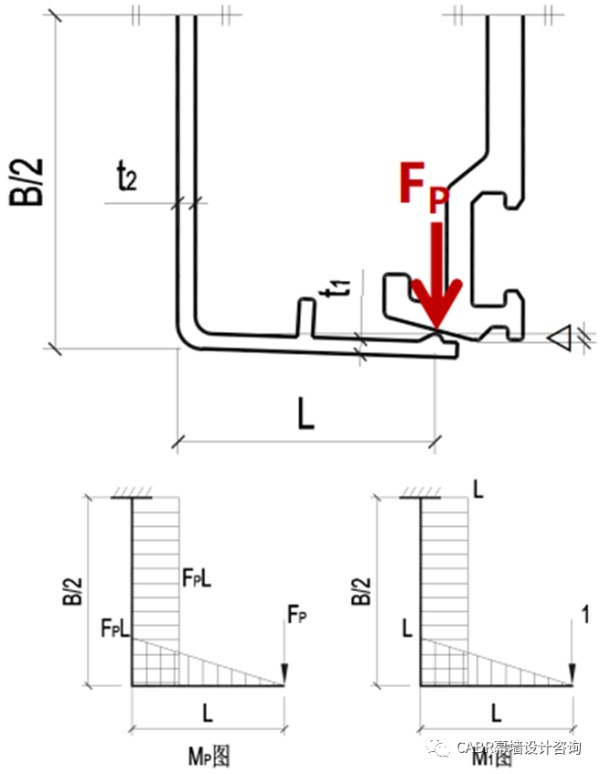
装配试验和拆卸试验的力—位移曲线与有限元模拟曲线对比发现,力与位移在初始阶段有台阶,之后几乎线性,峰值后大幅降低;装配力均值为344N、分离力682N,与有限元模拟结果非常接近。咬合型装饰扣盖和压板连接的承载力,主要与以图7所示几何参数有关:
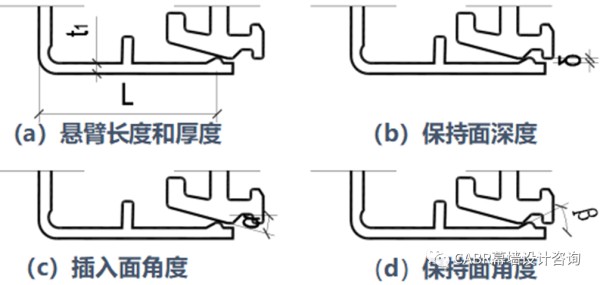
通过定性分析可知:咬合型装饰扣盖是一种典型的卡扣型连接;安装和分离过程,是悬臂钩的变形过程;插入面角度α,应尽可能的小,以减小装配力;保持面角度β,角度越陡,保持强度和分离力越大。以扣盖装配过程中的某一时刻做静力分析,假设悬臂钩为理想的悬臂梁,边界刚度无穷大,见图8。
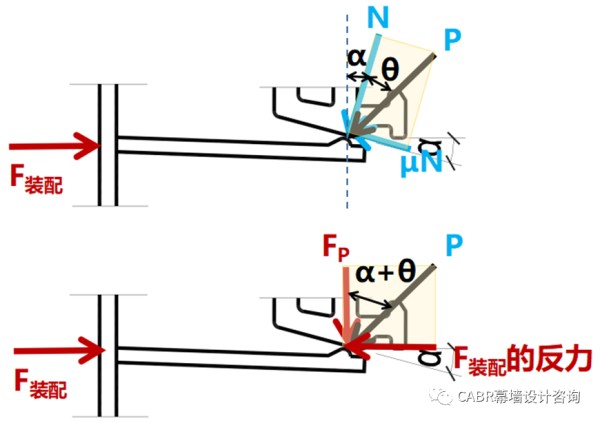
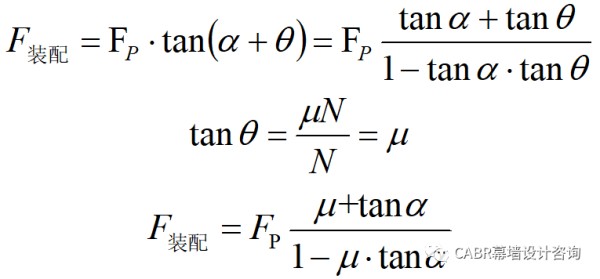
同理,对扣盖分离过程中的某一时刻可以做类似分析,可以得到:
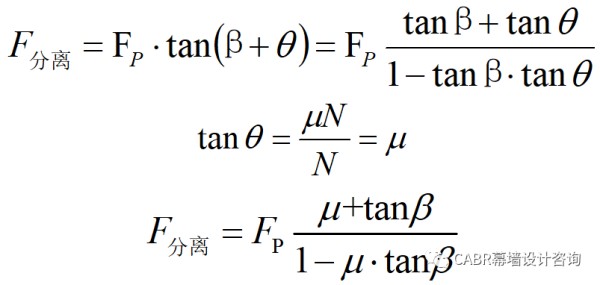
上述公式中,最重要的就是确定偏斜力Fp。通过结构力学的知识,可以求出Fp与悬臂钩变形的关系,见图9:
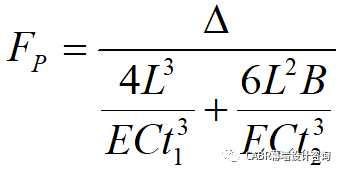
Fp ——偏斜力,使悬臂钩发生大小为Δ的竖向变形的力
C ——悬臂钩的截面宽度,
B——扣盖底板宽度
t1 ——悬臂钩根部厚度,
t2 ——底板厚度,
L ——悬臂段长度,
E ——弹性模量,
δ——保持面深度,
φ ——预变形角度,
Δ——悬臂钩竖向变形,Δ最大值与δ、L和φ有关
最后,对理论公式进行验证,将理论公式计算值与试验值进行对比,得到对于装配力和分离力,理论计算值与试验值的偏差分别为9.8%和5.9%,误差在可接受范围内,证明了理论公式的正确性。本文通过有限元模拟、试验测试和理论分析,对玻璃幕墙咬合型装饰扣盖破坏机理进行研究,给出了咬合型装饰扣盖的装配力和分离力理论计算公式。感谢江河创建集团股份有限公司对于本研究的大力支持!
作者简介:

王 超
中国建研院中建研科技工程咨询设计院幕墙所科研室主任,高级工程师,主要从事幕墙设计与研究工作。代表项目包括北京朝阳站、北京大运河博物馆、北京地铁7号线环球影城地铁站等;作为主要研究人员完成了各级科研项目10余项;参编行业、团体表3部;发表学术论文20余篇,其中EI收录3篇。








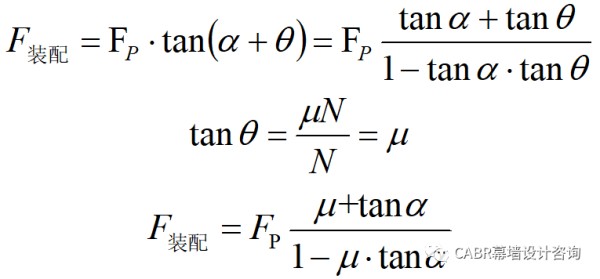
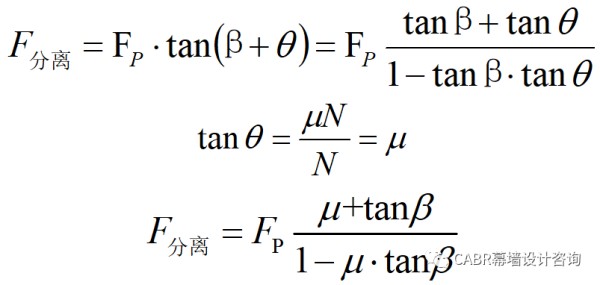

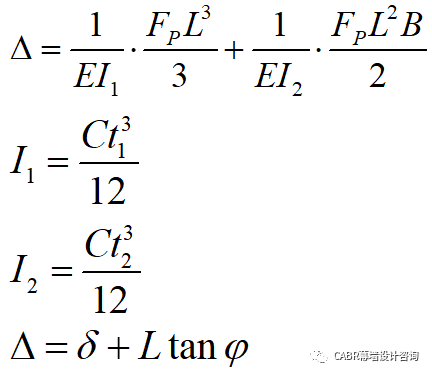
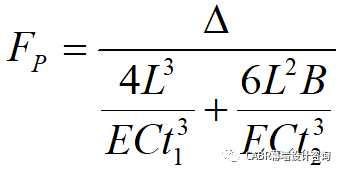



 公安机关备案号 110102000764
公安机关备案号 110102000764