---对标准的通读随想

　　河北胜达永强新型建材有限公司   姚春贵  刘秀云

　　JG/T180-2005《未增塑聚氯乙烯（PVC-U）塑料门》和JG/T140-2005《未增塑聚氯乙烯（PVC-U）塑料窗》两项标准，已于2006年1月1日起实施。在两项标准中都有一个附录D（资料性附录）——建筑外窗抗风压强度、挠度计算方法，它替代了原标准GB7106—88附录A建筑外窗抗风压强度、挠度计算方法。

　　在标准附录D中第D.5条，均给出了两个集中荷载图示及计算公式：

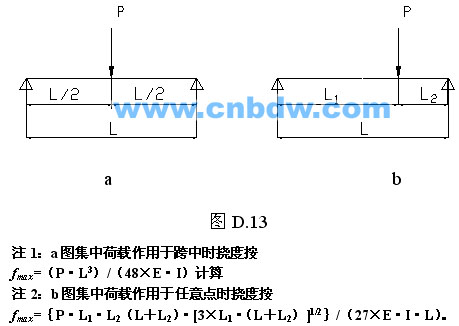
　　从集中荷载作用于简支梁形式上看，我们不难想象，即然图b为集中荷载作用于任意点时的情况，当然它也适用于荷载作用于中点时的情况，即包含当L1=L2= L/2时的情况，两公式应当有一定的内在联系。

　　从简单的道理上说，注2公式即然是集中荷载作用于简支梁任意点时的挠度公式，那么，当L1=L2= L/2时，任意点集中荷载挠度公式应当变为集中荷载作用于跨中时的挠度公式：

　　通过以上验算，首先从形式或公式格式上说明了注2公式对注1公式的可包容性。

　　为了从根本上找出两公式的内在联系，我们通过受力图试将该公式做一推导，并通过推导，进一步找出公式的简化规律，力求用一个通用公式表示它们。

　　如下图，一简支梁上有一集中力P作用，求梁支梁的最大挠度。

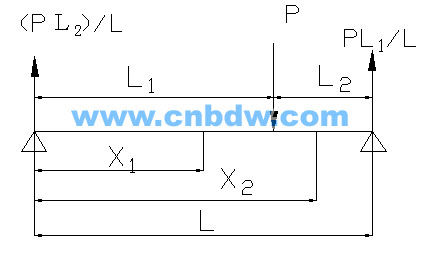
　　由材料力学，对于简支梁来说，如果全梁各截面的弯矩可用一个弯矩方程Mx来表示，则梁的挠度微分方程也只要用一个就可求出整个梁的挠曲线方程。而如果全梁各截面的弯矩不可用一个弯矩方程Mx来表示，则梁的挠度微分方程就不能用一个去求出整个梁的挠曲线方程。或者说，复杂的挠曲线是由若干段不同方程生成的曲线组成的。实际中我们发现，确有人直接取想象中的最大挠度所在截面的挠度微分方程一步求出整个梁的挠曲线方程，出现这种情况，其根源是对材料力学的理解得不够透彻。这段话虽然有点绕，但一定要慢慢细品。我们将要推导的受任意集中荷载简支梁的挠曲线方程，就是由两段组成的。

　　一、推导过程如下：

　　求解此梁的挠度，根据上述的说明，应将其分为两段（以力P的作用点为界）。

　　对于梁的左段，即当0≤X1≤L1时，其弯矩方程为：

　　Mx1=（P•L2/L）•X；设f1为梁左段的挠度，则由材料力学

　　E•I•f1／／=（P•L2/L）•X

　　积分得E•I•f1／=（P•L2/L）•X2/2＋C1--------------------------------（1）

　　二次积分：E•I•f1=（P•L2/L）•X3/6＋C1X＋D1--------------------（2）

　　由于X1等于零时简支梁的挠度f1等于零（边界条件），将X1=0代入（2）得D1=0

　　对于梁的右段，即当L1≤X2≤L时，其弯矩方程为

　　MX2=（P•L2/L）•X－P•（X－L1）；设f2为梁右段的挠度，则由材料力学

　　E•I•f2／／=（P•L2/L）•X－P?（X－L1）

　　积分得E•I•f2／=（P•L2/L）•X2/2－[P（X－L1）2/2]＋C2-----------------------（3）

　　二次积分：E•I•f2=[（P•L2/L）•X3/6]－[P•（X－L1）3/6]＋C2X＋D2------------（4）

　　公式（1）、（2）用于梁的左段，公式（3）、（4）用于梁的右段，积分常数C1、D1、C2、D2的确定需利用边界条件及在两段连接处（分界点）挠度相等（挠曲线的连续条件）和倾角相等（挠曲线的平滑条件）的条件，

　　①在X=0处，f1=0；

　　②在X=L1处，f1／= f2／（f1／、 f2／为挠曲线的倾角）；

　　③在X=L1处，f1= f2；

　　④在X=L处，f2=0；

　　由以上四条件求得（过程略）：C1= C2= -[（P•L2）/6 L]•（L2－L22）；D1=D2=0。

　　代入公式（1）、（2）、（3）、（4）整理即得：

　　对于左段   0≤X≤L1

　　E•I•f1／=（P•L2/L）•X2/2＋C1--------------------------（1）

　　= P•L2/6L •[3X2－（L2－L22）] --------------------------（5）

　　E•I•f1=（P•L2/L）•X3/6＋C1X＋D1--------------------（2）

　　= （P•L2/6×L）•[X3－X（L2－L22）]  ----------------------------（6）

　　对于右段  L1≤X≤L

　　E•I•f2／=（P•L2/L）•X2/2－[P•（X－L2）2/2]＋C2--------------------（3）

　　= （P•L2/6×L）•[3X2－（L2－L22）]-[ P/2•（X－L1）2]---------------（7）

　　E•I•f2=[（P?L2/L）•X3/6]－[P•（X－L1）3/6]＋C2X＋D2-----------------（4）

　　= （P•L2/6L）•[X3－X（L2－L22）] -[P/6•（X－L1）3]---------------（8）

　　由公式（5）、（6），能求左段各截面的倾角和挠度，由公式（7）、（8）两式，能求右段各截面的倾角和挠度。当然，推导计算时要注意X的取值范围，我们在这里强调X的取值范围，是因为发现有一篇文章在求简支梁挠度方程的积分常数时，比如C1 ，居然用X= L时f1=0去求解，而且还坚持认为：即然是变量，有何值不存在？按我们对公式的推导要求，只能取①在X=0处，f1=0；④在X=L处，f2=0；去求解相关积分常数；用X= L时f1=0去求解积分常数C1是没有意义的，也是错误的，因为X= L时，对“函数”式E•I•f1=（P•L2/L）•X3/6＋C1X＋D1来说不等于零，该“函数”在这里是一特定曲线和曲线段，这样做只能是证明作者对函数概念的模糊。

　　二、下面接着推导

　　梁的最大挠度是在倾角f /为零之处（从概念上说，不能认为梁的最大挠度在最大弯矩处），若L1＞L2，则最大挠度显然在左段内，命左段的倾角方程（5）f /等于零，即得最大挠度所在之位置，于是命：

　　P•L2 /6L•[3X2－（L2－L22）] =0

　　则：3X2－（L2－L22）= 0

　　得：X=[（L2－L22）/3]1/2  --------------------------------------（9）

　　将（9）式代入（6）式即得最大挠度

　　fmax= -[P•L2•（L2－L22）3/2]/ [9×31/2×L•E•I] --------------------------（10）

　　展开即得：

　　fmax=-｛（P•L1•L2•（L＋L2）•[3×L1•（L＋L2）]1/2）｝/（27×E•I•L）。

　　当然对于公式的推导过程，非专业人士可能不十分清楚，但是我们这样做，是给大家一个说明，该公式是有推导基础的，不是仅靠验证修改来证明的。

　　由公式的推导，笔者有以下进一步的建议，那就是，将计算挠度都归为挠曲轴的中点挠度，在此较具体详细地论证一下。所谓中点挠度公式，即不论简支梁所受的载荷形式如何，如三角形载荷、梯形载荷、复合形载荷、任意点集中载荷等等，我们求其挠度时，都用中点挠度代表最大挠度。原因如下：

　　（1）在上述集中载荷挠度公式的推导过程中，我们已经知道，最大挠度点的位置是：

　　X=[（L2－L22）/3]1/2  ------------------------------------------（9）

　　可以发现，在极限情况下，当P作用点接近于右支座时，即L2→0，将其代入（9）式得：X=L/31/2=0.577L。就是说，当载荷不在梁的中点时，最大挠度的位置实际上也很靠近中点，在极限情况下，最大挠度所在位置到中点的距离也只有0.077L。也可以说，非极限情况时，最大挠度所在位置基本就是中点。

　　（2）简支梁的挠曲线是一条平滑曲线，底部趋于平直，由于梁中点靠近最大挠度位置，故中点挠度的大小与最大挠度也十分相近（见后面计算比较）。在工程中为了简化计算，便常以中点的挠度作为最大挠度。

　　（3）塑料门窗的抗风压强度计算中，主受力杆件往往受多个力图作用，总挠度是由多个挠度因子相加而得，它们的最大挠度值有的就是中点挠度，比如中心对称梯形载荷；有的不是中点挠度，比如任意点集中载荷，就是说它们的最大挠度值不在一条直线上。而根据力图相加原理，相加力图必须在一条直线上。由此我们认为，从理论上说，多个挠度因子相加，只有中点挠度因子是在同一直线上，相加才有意义。

　　（4）对于复合荷载图形挠度公式的推导，求最大挠度点X时，往往需要解高次方程，增加了解题难度（见后面例题）。

　　因此最合理的挠度和值应是各挠度因子的中点挠度之和。

　　有了这种思路，我们首先就可以将前面的两个集中荷载公式归纳为一个通用公式，并用中点挠度表示之，因为任意点集中载荷包容了作用于跨中的集中荷载，或者说作用于跨中的集中荷载只是任意点集中载荷当L1=L2= L/2时的特殊情况。

　　将X= L/2代入左段挠度公式

　　E•I•f1= [（P•L2）/（6×L）]•[X3－X（L2－L22）]  ----------------（6）

　　得梁的中点挠度为：fL/2= -[（P•L2）/（48×E•I）]•（3L2－4L22）（L2指小端）-----（11）

　　这样我们就避开了解方程求最大挠度点X了，而直接指定X= L/2。非常简便。

　　我们再看该公式的包容性：当L2= L/2时，代入公式（11），得：

　　fL/2=-[（P•L/2）/（48E•I）]•（3L2－4•L2/4）= -P•L3/48E•I（变成集中荷载作用于跨中时的挠度公式）

　　因此我们只要记住一个“梁承受任意点集中载荷时的中点挠度公式”：

　　fL/2=- [（P•L2）/（48E•I）]•（3L2－4L22）（L2指小端）--------（11）

　　就可以解决梁承受集中载荷时的各种情况的计算，包括对称荷载。避免了集中荷载作用于任意点时挠度公式的复杂性、不好记忆性、L1与L2的不易分辨性，由于公式的简化，也会减少印刷、校对的失误。

　　......