断桥隔热铝型材是一种符合节能潮流的节能建材，当它用于建筑幕墙和铝合金外窗时，除了要考虑其保温断热性能之外，还要充分考虑到其结构的安全性和可靠性。因此断桥隔热铝材用于建筑幕墙和铝门窗的结构件时，应进行强度、刚度设计计算， 由于断桥隔热铝型材是由两种不同材料组合成的型材，怎么样去科学、准确地校核其强度和刚度，是一个比较复杂的问题，目前有关的国内规范并没有明确的计算方法。审图时，有的审图单位要求只取室内侧（隔热条以内）铝型材作为受力单元；而有的则同意隔热条两侧铝型材都可以作为受力单元进行计算。究竟那种意见更合理呢？大家知道，要计算构件的强度和刚度，必定要计算其截面特性，其中，主要是惯性矩及抵抗矩。本文就从计算断桥隔热铝型材截面的惯性矩及抵抗矩入手，按照材料力学中组合梁的计算原理以及JG/T 175-2005《建筑用隔热铝合金型材  穿条式》附录B提供的计算截面惯性矩的公式，给出两种计算不同材料组合的型材截面的惯性矩、抵抗矩方法，并对其进行分析、对比，为工程实际设计时提供参考。

　　一、两种计算组合型材截面惯性矩、抵抗矩的方法

　　方法一：按照材料力学中组合梁结构进行计算，将其中一种材料转化为另一种材料，一般将隔热条等效为铝条，变成统一的铝截面，求出等效截面的惯性矩、抵抗矩。

　　1、计算原则  

　　①、断桥隔热铝型材截面的一部分是隔热条，在结合良好的加工条件下，可以认为隔热条与铝型材在变形前后保持平截面，应变ε线性分布。 

　　②、两种材料弹性模量不同，所以在相同应变ε时，应力相差n倍，n为弹性模量之比： n=E1/E2

　　式中 E1：铝型材的弹性模量 

　　E2：隔热条的弹性模量 

　　③、可以将复合截面按弹性模量比转化为单一材料的等效截面，计算出应力、挠度，隔热条部分的应力还须转化为原材料的应力。

　　2、求出等效铝截面  

　　将复合截面转化为单一的铝截面，基本原则是将隔热条截面厚度缩小为原来的1/n。因为厚度的缩小对截面的特性如面积A，惯性矩I，截面抵抗矩W的影响是线性变化的，恰好与弹性模量E的变化相补偿。即te=t2/n/ 

　　式中 te：隔热条等效厚度
　　t2：隔热条的实际厚度
　　n：铝型材与隔热条弹性模量之比  

　　3、等效截面惯性矩及抵抗矩的计算  

　　转化为统一的铝材等效截面后，根据材料力学的知识，或采用软件可很方便的计算出其惯性矩及抵抗矩。

　　方法二：按JG/T 175-2005附录B提供的计算截面惯性矩的公式。

　　Ief=IS（1-ν）/（1-ν×C）
　　IS=  I1+I2+A1a1^2+A2a2^2 
　　ν=（A1a1^2+A2a2^2）/IS
　　λ^2=c×a^2×l^2/（E×IS×ν×（1-ν））
　　C=λ^2/（π^2+λ^2）
　　Wef=Ief/Z

　　式中：     Ief  ―有效惯性矩(单位为cm4)；
　　Is ―  刚性惯性矩(单位为cm4)；
　　ν ― 刚性惯性矩的组合参数；
　　C  ―  弹性结合作用参数；
　　λ ― 几何形状参数；
　　l ―  梁的跨度(单位为cm)；
　　c  ―  组合弹性值(单位为N/mm2)；
　　E ―   组合弹性模量(单位为N/mm2)；
　　A1 ―  A1区的截面积(单位为cm2)；
　　A2 ―  A2区的截面积(单位为cm2)；
　　a 1 ― A1区形心到隔热型材形心的距离(单位为cm
　　a 2 ―  A2区形心到隔热型材形心的距离(单位为cm)；
　　I1 ―   A1区型材惯性矩(单位为cm4)；
　　I2 ―   A2区型材惯性矩(单位为cm4)。

　　注： 因为λ取决于梁的跨度，所以有效惯性矩是跨度的函数。对于大的跨度其值则接近刚性值。

 

　　二、计算实例

　　用二条截面厚度为2高为12的PA66GF65隔热条（E=2900N/mm^2）将二根40*20壁厚为2的铝合金矩形管（E=70000N/mm^2）组合成隔热铝型材（如下图）

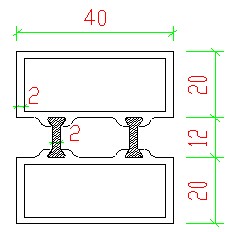
　　根据方法一，可以将隔热条宽缩小70000/2900=24.14倍后生成“铝质等效截面”，然后计算出等效截面的惯性矩及抵抗矩。即将尼龙条宽度原2+2改为（2+2）/24.14=0.17后生成铝质等效截面如下图。

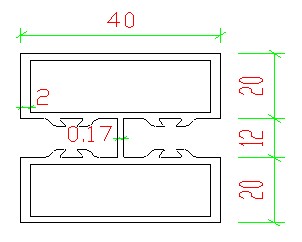
　　根据等效截面图，采用计算软件可求出等效截面惯性矩I、抵抗矩w：

　　I=144590  mm4
　　w=5561  mm3

　　根据方法二， 在E=70000N/mm^2，c=80 N/mm^2，l=1000mm的条件下，计算过程如下：

　　A1=248 mm^2         I1=17100 mm^4        a1=16 mm
　　A2=248 mm^2         I2=17100 mm^4       a2=16 mm
　　E=70000 N/mm^2     l=1000 mm           c=80 N/mm^2
　　IS=  I1+I2+A1a1^2+A2a2^2 =2×17100+2×248×16^2 = 161176mm^4
　　ν=（A1a1^2+A2a2^2）/IS =（2×248×16^2）/161176 = 0.788
　　λ^2=c×a^2×l^2/（E×IS×ν×（1-ν））
　　=80×32^2×1000^2/（70000×161176×0.788×（1-0.788））
　　=43.46
　　C=λ^2/（π^2+λ^2）=43.46 /（3.14^2+43.46）=0.815
　　Ief=IS?（1-ν）/（1-ν×C）
　　=161176×（1-0.788）/（1-0.788×0.815）
　　= 95503mm^4
　　Wef=Ief/Z=95503/26= 3673mm3

　　三、两种计算方法的比较和分析

　　从以上实例可以看出，计算方法不同，其计算结果也不一样，两种方法算出来的惯性矩相差144590/95503=1.51倍。造成这种差异的主要原因在于方法一是假定隔热条与铝型材在变形前后保持平截面，应变ε线性分布。但实际上胶条是有切向变形的，这种变形类似于隐框玻璃板块中竖向结构胶在玻璃自重作用下产生的切向变形，而这种变形使得变形前杆件的某一横截面，在变形后己不处于同一平面了。也就是说，胶条的纵向剪切变形会影响组合型材的惯性矩Ief的数值。但要直接将这二者建立数学关系则是十分困难的。我们可从以上的分析和计算过程得出，影响组合型材惯性矩的因素有：

　　1、胶条的E值，E值越小，胶条的纵向剪切变形越大，用等效截面计算的惯性矩值误差越大。

　　2、胶条的高度，胶条越高，胶条的纵向剪切变形越大，用等效截面计算的惯性矩值误差越大。

　　3、胶条的厚度，胶条厚度越小，胶条的纵向剪切变形越大，用等效截面计算的惯性矩值误差越大。

　　4、梁的跨度，跨度越大，胶条的应变越小，用等效截面计算的惯性矩值误差越小，在上述算例中，如果把梁跨度l=1000mm改为l=2000mm，则两种方法计算出来的结果差异从1.51倍降为1.20倍。

　　四、结论：

　　1、可通过求断桥隔热型材复合截面的截面特性，按一般构件的计算方法算出型材的应力和挠度，断热条应力为按等效截面计算的应力除以弹性模量比n。

　　2、方法一，计算方法简单，只要画出等效截面就可用软件，方便、快速地求出其惯性矩、抵抗矩，进而计算出型材的强度和刚度，但其计算结果偏于不安全；方法二，计算要依赖于很多参数，计算过程复杂，计算结果偏于保守。 

　　3、从工程的安全角度出发，在施工设计时，建议用第二种方法来计算隔热型材截面特性、及其强度等。在方案设计阶段，可考虑采用第一种方法来估算隔热型材截面的大小，特别是在梁的跨度、胶条的截面厚度较大，而胶条的截面高度较小的情况下，可获得较为准确的结果和较高的工作效率。