在我国，每年平均幕墙建筑面积约为800万平方米，其中框架式和大单元式结构比例约占60%，即480万平方米，按平均第平米用去铝合金型材重量为13-22kg/m²计算，需要75万吨铝合金型材，考虑到大单元用量还要大，实际上约22kg/m²（其中大单元系结构占有率约为20%）。

　　本文真实的幕墙设计例子加以说明，原设计幕墙为框架式连续双跨梁支撑的力学模型，后经优化计算改为多跨铰接静定梁支撑力学模型后，得到了不同的节约型材的效果，过去对常规框架式幕墙设计，往往在计算立柱强度、刚度时，往往是以幕墙所在最高的位置风压为风荷载标准值（或乘以1.4的系数为设计值），其他任何高度均以此风压设计值或标准值做为强度、刚度计算依据。这种确定风荷载方法是不科学的。

　　显然，在最高处的幕墙结构立柱，满足强度小于铝合金（或钢型材）型材所给出的材料许应力值时，就认为强度、刚度满足了规范规定。那么一座100-200m以上的幕墙在低高度时型材与超高层型材一样的几何尺寸，那么会产生惊人的浪费资源，也意味着浪费大量电能，因为铝生成用电解法，相当费电的。

　　这里有一个优化设计概念问题，在强度计算时，一定要考虑两个因素：强度、刚度剩余系数概念；要考虑等强度、等刚度的设计原理。

　　笔者认为强度剩余系数，是指强度与材料许应力值、设计计算值之比值，称为剩余强度系数，一般可以取1.15即可。

　　幕墙安全设计第二个概念是指等强度、等刚度设计理念，规范中规定铝合金骨架刚度值设计限定为1/180，并未指出就在幕墙最高处的值，对整个幕墙分段高度均有效，即都要满足1/180的概念。当然，我们要引入第一个概念的剩余刚度系数和剩余强度系数，是考虑保守、安全一些。例如：一栋建筑外墙立面为框架式幕墙H=40m，层高H=4.6m，在银川市内地面粗糙度为B类，基础风压W=0.65KN/m2，材料6063AT5，材料设计许应力为124Mpa，由下列表A列入本幕墙从难从10m标高到40m时设计，标准风压值见表A

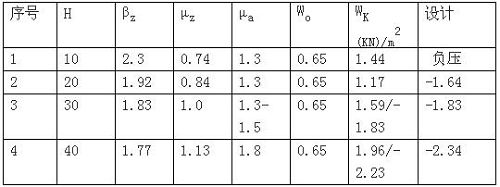
　　目前95%以上的幕墙公司在投标方案设计时，往往取H=40m,Wk1=1.96 KN/m2为标准值和Wk1=-2.34KN/m2设计值进刚度和强度计算的。

　　从表A中40m处，我们清楚看出框架式幕墙风压标准值为1.86 KN/m2设计值为2.74 KN/m2；在高度为40m时，标准风压值为1.96 KN/m²，设计值2.74KN/m²，H=40m，根据幕墙设计主要以刚度准则原则，即满足各分高区段都满足刚度。

　　用不同高度即H=30m, H=40m,的风压W30，W40，对其强度计算，并满足f20=f30=f40，称等刚度设计准则。因为，立柱挠度fi=awihwh/E.Jx，显然挠度与Jx成反比，而Jx=f(Wk)为函数关系，也就是挠度与Jx成反比，而Wk成正比，所以在40m高全段中，我们可以分0-20m,20m-40m，二段分别设计满足各段之挠度，f20=f30=f40≤1/180，并得到二段的风压值：1.64、1.83、2.14，使用在各段铝合金型材在外型保持一致时，可以用不同Jx值的型材断面，当型材Jx较小时，断面可以减少达到节省铝材、降低成本。

　　例如：在30m高度上铝型材比在设计40m处型材惯性矩高21%，Jx40/Jx30=2.34/1.83=1.21考虑其他非主柱结构用料比例，立柱型材实际采用等强度、等刚度设计中的成本可降约9%，Jx40/Jx30比例折减系数近为0.75，即实际是高出9%，此数据为选定最低降低成本之比例率。

　　上述是采用等强度、等刚度设计的情况（即分层计算分压计算之效果），下面重点举银川市代建办候利军总工提议采用多点铰接静定连续梁的实例，来降低型材成本与设计计算，幕墙立柱结构支撑体系的力学模型状态有关，计算是尽量建立多跨静态连续铰接梁的力学计算模型。例如：幕墙立住是简支梁架、支撑体系、双跨连续梁力学支撑体系模型，还是多点跨铰接静定力学模型，其三种力学模型所使用铝型材降低成本是不同的。（当然对钢结构桁架系统、钢架系统）的力学模型有所不同。这里引入并参考了“幕墙立柱支撑体系与数据分析”一文中的论述，可以从银川国际会展中心的实例定量看出不同支撑的力学模型对节省铝型材成本的潜力很大。

　　这里我们将讨论框架支撑体系的力学模型关系，及其应用。

　　外围护结构的幕墙体系按安装方式可分为框架式、单元式、拉杆驳接式、索式驳接式等几大体系，现分述如下：

　　1．框架式幕墙

　　这种支撑方式的幕墙是最典型的，已有很长时间的历史，且现在的幕墙工程中近60%以上经常应用。该种幕墙体系制造成本较低，工期较长，由于装饰面完成后需要现场打胶封闭，因此冬季施工时，由于胶的作业温度限制导致北方地区的幕墙将不能施工。

　　2．单元式幕墙（含双层热通道幕墙的结构）

　　单元式幕墙构成及安装方式较框架式有更多的优点，但相对于框架式幕墙来说成本相对较高，通常大单元尺寸均为横向一个装饰分格，竖向为一个层间尺度，由于这些大单元均在加工厂内加工制作，因此集成化程度非常高，能达到相当高的安装精度，由于现场不需要进行龙骨布置，因此可以与主体结构同步施工，大大缩小了施工周期，为业主赢得了更多的宝贵时间。拉杆、拉索式……。

　　幕墙的几种形式，从完成后的外饰效果来看没有什么不同但内部结构及设计理念却有着深刻的不同，这里可认为大单元、上下左右插接、吊挂单元上部、插接形式或设成多跨连续铰支梁形式，仍可以和框架多点铰支梁计算，框架可按多点铰支梁计算，框架可按多点连续的计算更好的合理性。

　　目前较为流行的小单元式幕墙实际上是一种框架式幕墙的变种，其设计过程中渗透了单元式幕墙思路，也就是把装饰面材内侧增加挂式附框，直接挂于主体框架之上，虽增加了可拆卸性，但由于其依然具有先行安装网格式幕墙支撑龙骨，因此仍然把小单元划归为框架式幕墙的范畴是很合适的。

　　无论框架式幕墙，单元式幕墙其支撑体系的力学模型都是一致的，现分述如下：

　　1． 简支梁力学模型（见附图）
　　2． 连续（双跨）梁力学模型（见附图）
　　3． 多跨铰接静定梁力学模型（见附图）

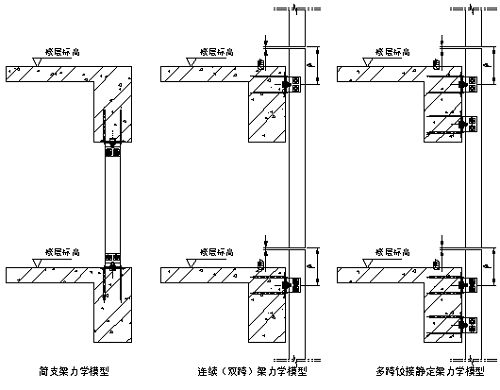
　　以上三种立柱力学模型很好的概括了幕墙常用结构。

　　简支梁力学模型常用于幕墙结构嵌入主体结构中，此时的幕墙计算模型是没有任何选择余地的，是由主体结构决定的。

　　连续（双跨）梁力学模型是最为常用的幕墙计算模型，此时幕墙体系悬挂于主体结构之外，每层铝立柱由铝插芯插接串联，该连接点处且可以延立柱轴向滑动，这样的结构便构成了连续的规律排布的梁体，无论框架式幕墙还是单元式幕墙在本种支撑体系上是均可以实现的，也就是说两种幕墙体系在这种力学模型下完全统一了。

　　有的时候虽然完全满足把幕墙支撑体系设计成连续（双跨）梁力学模型，但我们却把他设计成多跨铰接静定梁力学模型，是因为此时如果把它设计成连续（双跨）梁力学模型并不是最经济合理的，那么这种情况何时会发生呢？大跨度层高，大分格，且梁体有足够的高度，这三个条件的交集便是经常设计成多跨铰接静定梁力学模型的必要条件。

　　这三种力学模型作为幕墙结构设计中的最基本的元素并不是由设计师随意决定的，设计师必须统一规划所设计的幕墙体系，研究建筑主体结构所提供的边界条件，最终确定。因为它直接关系着幕墙的每平米比重，也就是说直接影响到幕墙的造价，从设计本身来讲，也就是如何达到一个“等强度设计”的一流境界的问题。

　　从定性方面来看，在相同的外界条件下，这三种力学模型中简支梁力学模型立柱最为费料，多跨铰接静定梁力学模型立柱最为省料，但多跨铰接静定梁力学模型由于增加了一个支点,导致了预埋件的费用的增加，人工费的发生，成本也有所增加。在幕墙结构设计中，相对来说连续（双跨）梁力学模型最能达到既节省材料成本，也能达到降低人工费用的目的。

　　上述三种力学模型在达到某种特定的边界条件时，其中一种模型会近似另一种模型，其并没有一个明确的分界值，完全取决于其构造特点。

　　下面我们一定量的方式加以说明，以数字的方式阐述：

　　又例如北京地区，C类，8度抗震，计算高度120米，中空玻璃（取500N/m2）,楼层高度3.6米，横向分格1.48米，试按　　三种力学模型进行铝立柱（6063T5、GB5237-2004）分析，对计算结果进行比较。

　　由《玻璃幕墙工程技术规范》（JGJ102-2003）和《建筑结构荷载规范》（GB50009-2001（2006年版））：

　　阵风系数1.640；高度变化系数1.538；风压组合值1.362K N/m²

　　地震力组合值0.400K N/m²

　　风荷载与地震力组合标准值1.362K N/m2；风荷载与地震力组合设计值2.167K N/m²

　　则，铝立柱所受设计线荷载q设计=2.167x1.480=3.20716N/mm

　　铝立柱所受标准线荷载q设计=1.362x1.480=2.01576N/mm

　　轴力N=500x3.6x1.48=2664(N)

　　（一）按简支梁力学模型分析:

　　弯矩： =5195599.2 Nmm --------(A)
　　挠度： =12.1mm<20mm≤1/180-----(B)
　　由不等式(B)得： I >3148905.086 mm4
　　=83.68<124N/mm2-----（C）
　　由不等式（C）得Wmin >59132.05457 mm3

　　可见，幕墙铝立柱的截面特性Imin >3148905.086 mm4; Wmin >59132.05457 mm3，在CAD中可以发现矩形界面70x180x3满足要求，I= 5923872mm4;W=65820.8 mm3，A= 1464 mm2可见是应力控制的截面。

　　（二）按连续（双跨）梁力学模型分析:

　　我们借助美国有限元分析程序Frame进行分析，思路为我们把按简支梁力学模型计算出的最小截面特性输入程序比较结果是否富余或超标，并进行修正。还有一个重要问题，就是连续梁连接插芯的问题，据查现行规范《玻璃幕墙工程技术规范》JGJ102-2003第138页原文如下“立柱自上而下是全长贯通的，每层之间通过滑动接头连接，这一接头可以承受水平剪力，但只有当芯柱的惯性矩与外柱相同或较大且插入足够深度时，才能认为是连续的，否则应按铰接考虑。”人们一般认为插芯连接处是可以传递弯矩的，于是对芯柱的惯性矩进行了规定，但如果它传递了弯矩那么由于滑动连接，此处的接触应力又变得极其复杂是一个高尖端的学术课题，况且如果考虑芯柱的惯性矩的规定，芯柱又大的难以接受，增加了很大一部分成本。那么怎样解决这样一个技术的问题呢？仔细研究这句话可以看出他有另一种叙述：“这一接头可以承受水平剪力”那么如果让这一接头只承受剪力，而不承受弯矩（就是该处的弯矩为零）是不是就能很好地解决这一问题呢？根据这一想法，我们图形解决如下：（我们暂定H=300mm，H的意义参见力学模型（图一-图四）所示

　　杆件的截面特性（参见简支梁反推的截面特性）（图一）

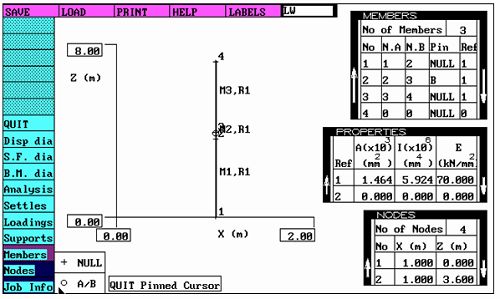
　　连续（双跨）梁力学模型弯矩分布图（图二）

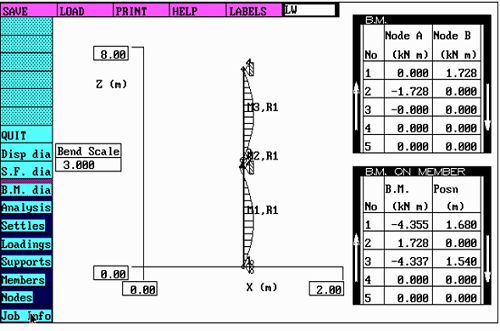
　　连续（双跨）梁力学模型挠度分布图（图三）

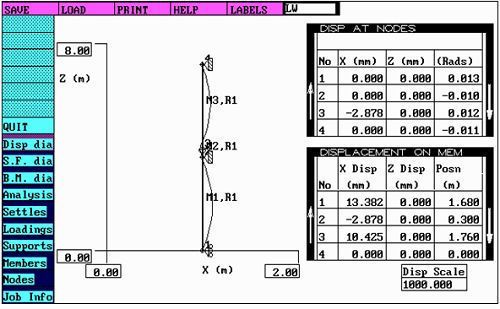
　　连续（双跨）梁力学模型支点支反力（图四）

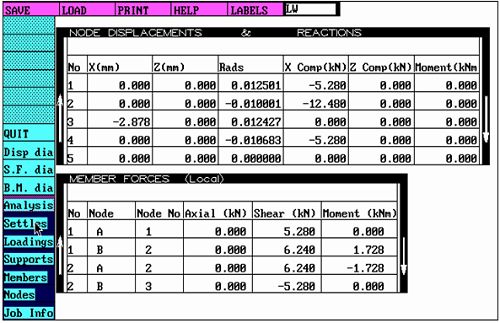
　　从上面的连续（双跨）梁力学模型有限元分析（图二）的结果可以看出：

　　在同一样截面的立柱型材，同样受风荷载的前提下，简支梁的Wx为59132mm3，而采用（双跨）梁的结果Wx值为65820mm3，显然它大于简支梁Wx为59132mm3，那么简支梁比双梁比双跨梁应力大

　　同样受力同样型材断面，其简支梁比双跨梁挠度大f双-f简支=12.1-9.56=2.54mm，是以证明在同样受力和同样型材截面、同样层高条件下，采用不同的立柱支撑条件（简支梁，双跨铰接连续梁）其得到不同的型材几何截面积，可以清楚看出双跨梁对节约铝型材重量比简支梁情况省10%。

　　（三）多跨铰接静定梁力学模型分析

　　杆件的截面特性（参见简支梁反推的截面特性）（图五）

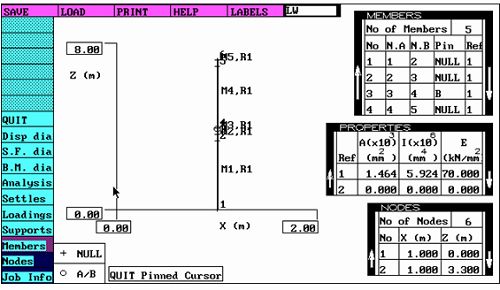
　　多跨铰接静定梁力学模型弯矩分布图（图六）

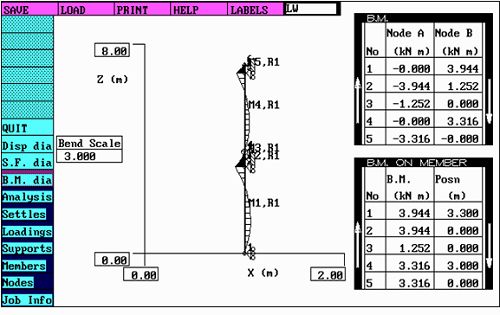
　　多跨铰接静定梁力学模型挠度分布图（图七）

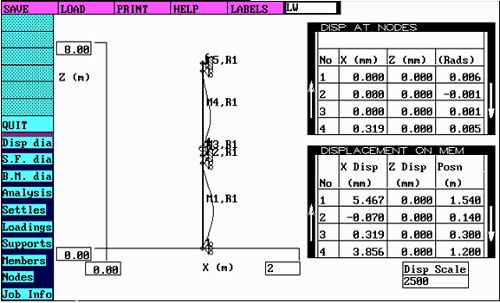
　　多跨铰接静定梁力学模型支点支反力（图八）

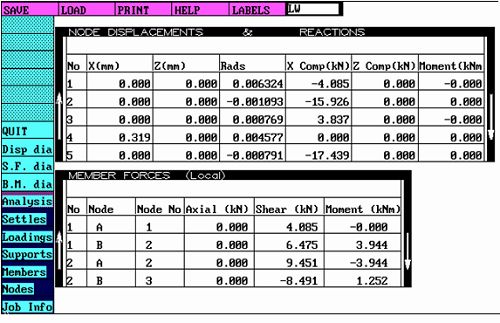
　　从上面的多跨铰接静定梁力学模型有限元分析（图六）的结果可以看出：

　　第三种支撑的多跨静定梁应力58.9Mpa挠度为3.9mm，它又比双跨梁在应力83.7和挠度9.56mm都低很多。

　　以上三种力学模型的受力分析后,从数据上定量的看出，在同等外界荷载下当简支梁力学模型安全性几乎到到极限时，连续（双跨）梁力学模型却有很大的余量，而多跨铰接静定梁力学模型拥有更多的余量，从而证明了在“等强度“设计时简支梁力学模型最费料，多跨铰接静定梁力学模型最省料，但从经济方面考虑连续（双跨）梁力学模型，也许是我们最好的选择。

　　我们也可以发现插芯连接处的弯矩均为零，这时插芯只承受剪切力可以不必做得很大了，降低了成本，也使得传力清晰合理。

　　有一个问题：这三种力学模型之间有什么关系吗？在什么情况下能够发生相互转化呢？经过大量的数据分析发现，当层高H值小到一定的程度时由连续（双跨）梁力学模型所计算的结果，非常接近简支梁力学模型计算的结果，另多跨铰接静定梁力学模型的两个支点间距小到一定程度时由多跨铰接静定梁力学模型所计算的结果，非常接近连续（双跨）梁力学模型计算的结果，也就是说三种力学模型存在着某种内在关系，笔者试图能够把他们在更基本的情况下进行统一。

　　还有一点需要指出的是，连续（双跨）梁力学模型的层高H值是一个变量，当H值增大到一定程度时，柱型材本身的应力，及挠度都会增大，而当H值减小到一定程度时，梁本身的应力，及挠度也会增大，也就是说在某种情况下，连续（双跨）梁力学模型总会有一个最合适的层高H值使梁的截面达到最小，可是有时候由于室内效果的要求，不能保证最合适的层高H值，那样我们等强度设计也能求得一个平衡值。一个优秀的幕墙设计师对幕墙结构的数学分析应该有所认识，这样我们才能设计出更优秀的产品。框架式纵向受力骨架的评估：本文提出二种方法优化设计可以同时协调采用这种优化设计，将平均使用框架式幕墙铝合金受力型材重量降低至少10-15%，一个幕墙若用型材总量300T可以省下45T按每吨3万元/T计算可省135万元。

　　当然仍有潜力可控，例如使用高强度的6061/T6型材有可以降低成本。本文供从事幕墙结构设计人员参考。本例使用6063T5，强度85Mpa；使用6063AT5，强度124Mpa，更好优化节省型材。

　　在优化框架式幕墙的铝合金型材方法较多，下面一种方法是充分利用GB50009-2001（2006年版）强制性条文，使设计计算中采用杆系与横框组合效应考虑时，因受力模型作用，双梯型荷载分布或矩型均布或其他类型等，可以利用η衰减系数修正。

　　还可以得到减少材料的结果，η—不同从属面积下的支撑面板柱横梁等，当从属面积大于或等于1m2时η值为0.8，当从属面积1m2-10m2要按表A值给出体型系数η的折减系数。（详见《建筑结构荷载规范》GB50009-2001（2006年版））折减系数是针对幕墙立柱、横梁和窗之中庭计算时，要对体型系数做插值求衰减系数时按下表A：

　　参考文献：
　　1．GB50009-2001（2006年版）《建筑结构荷载规范》
　　2．GB50011-2001《建筑抗震设计规范》
　　3．JGJ102-2003《玻璃幕墙工程技术规范》
　　4．幕墙结构优化设计——莫英光、焦杰
　　5．银川国际会展中心幕墙结构优化实例——银川市政府代建办总工候利军【完】